TREE

There are many applications in real life situations that make use of non-linear data structures such as graphs and trees. But our main concern here is a tree. Trees are one of the most important data structures in computer science. 

Trees are very flexible, versatile, and powerful data structures that can be used to represent data items processing hierarchical relationship between the grandfather and his descendants and in turn their descendants and so on.

TREE

A tree is a non-linear data structure in which items are arranged in a sorted sequence. It is used to represent hierarchical relationship existing amongst several data items. 

The graph-theoretic definition of a tree is: it is a finite set of one or more data items (nodes) such that

1. There is a special data item called the root of the tree. 
2. And its remaining data items are partitioned into a number of mutually exclusive (i.e., disjoint) subsets, each of which is itself a tree. And they are called subtrees.

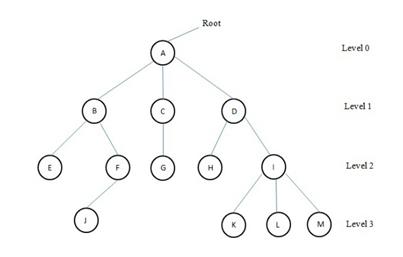
TREE TERMINOLOGY

There is a number of terms associated with the trees which are listed below:

• Root

• Node

• Degree of a node

• Degree of a tree

• Terminal node(s)

• Non-terminal node(s)

• Siblings

• Level

• Edge

• Path

• Depth

• Forest

1. Root: It is specially designed data item in a tree. It is the first in the hierarchical arrangement of data items. In the above tree, A is the root item.

2. Node: Each data item in a tree is called a node. It is the basic structure in a tree. It specifies the data information and links (branches) to other data items. There are 13 nodes in the above tree.

3. Degree of a node: It is the number of subtrees of a node in the given tree:

• The degree of node A is 3

• The degree of node C is 1

• The degree of node B is 2

• The degree of node H is 0

• The degree of node I is 3.

4. Degree of a tree: It is the maximum degree of nodes in a given tree. In the above, the node A has degree 3 and another node I am also having its degree 3. In all this value is the maximum. So, the degree of the above tree is 3.

5. Terminal node: A node with degree 0 is called a terminal node or a leaf. In the above tree, there are 7 terminal nodes. They are E, J, G, H, K, L, and M.

6. Non-terminal node: Any node (except the root node) whose degree is not zero is called non-terminal node. Non-terminal nodes are the intermediate nodes in traversing the given tree from its root node to the terminal nodes (leaves). There are 5 non-terminal nodes.

7. Siblings: The children nodes of a given parent node are called siblings. They are also called brothers. In the above tree

• E and F are siblings of parent node B.

• K, L, and M are siblings of parent node I.

8. Level: The entire tree structure is leveled in such a way that the root node is always at level 0. Then, its immediate children are at level 1 and their immediate children are at level 2 and so on up to the terminal nodes. In general, if a node is at level n, then its children will be at level n + 1. In the 4 levels.

9. Edge: It is a connecting line between two nodes. That is, the line drawn from one node to another node is called an edge.

10. Path: It is a sequence of consecutive edges from the source node to the destination node. In the above tree, the path between A and J is given by the node pairs. 
(A, B),(B,F) and (F,J)

11. Depth: It is the maximum level of any node in the given tree. In the above tree, the root node A has the maximum level. This is the number of levels one can descend the tree from its root to the terminal nodes (leaves). The term height is also used to denote the depth.

12. Forest: It is a set of disjoint trees. In a given tree, if you remove its root node ten it becomes a forest. In the above tree, there is a forest with three trees.