Data Structure With C
- INTRODUCTION TO DS
- ALGORITHMS
- ASYMPTOTIC ANALYSIS
- DYNAMIC PROGRAMMING
- DIVIDE AND CONQUER
- Arrays
- Linked List
- STACK
- EXPRESSION PARSING
- Queue
- GRAPHS
- TREE
- SEARCHING TECHNIQUES
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- SORTING
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Recursion
- Backtracking
- Hashing
Multi-Dimensional Array
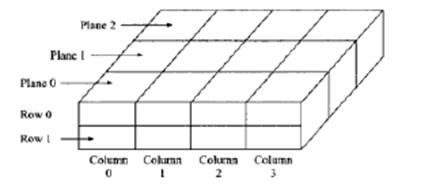
The arrays can also have more than two dimensions. For example, a three dimensional array may be declared as.
int myarray[3][2][4];An element of this array is referenced by three subscripts. The first specifies the plane number, the second specifies the row number and the last one is column number. Such an array is useful when the value is determined by three inputs.
The number of elements in any array is the product of the ranges of all its dimensions. For example, myarray contains 3*2*4 = 240 elements. The int myarray[3][2][4]; can be represented as shown as
JOIN TUTORIALS LINK
Our Newsletter Will Let You Know When Any New
Articles, Tutorials and Video Are Released.
CONTRIBUTE
MOBILE APP
Google Play
Copyright © 2026. All Rights Reserved.