Infix to Postfix Conversion

Infix to postfix conversion: The following algorithm transform the infix expression into equivalent postfix expression. The algorithm uses stack to temporarily hold operators and left parenthesis. The postfix expression will be constructed left to right using operands from infix expression and operator which are removed from stack. We begin by pushing left parenthesis onto stack and adding a right parenthesis at the end of infix expression.

The algorithm is terminated when stack is empty.

1. Create a stack
2. for each character ‘t’ in the input stream {if (t is an operand) output t

• else if (t is a right parentheses){POP and output tokens until a left parentheses is popped(but do not output)}
• else {POP and output tokens until one of lower priority than t is encountered or a left parentheses is encounteredor the stack is empty PUSH t}

     3. POP and output tokens until the stack is empty.

For better understanding, let us trace out an example A * B – (C + D) +E

So final POSTFIX Expression : AB*CD+-E+

Evaluation of POSTFIX Expression: A postfix expression itself determines the precedence of operators . It is easier for a machine to execute a postfix expression than an infix expression.

A postfix expression is without parenthesis and can be evaluated as two operands and operator at a time, this becomes easier for the compiler and the computer to handle. Evaluation rule of a postfix expression states:

While reading the expression from left to right, push the element into the stack if it is an operand; pop the two operands from the stack, if the element is an operator except NOT operator. In case it is NOT an operator, pop one operand from the stack and then evaluate it. Push back the results of the evaluation.

Repeat it till the end of stack.

1. Scan the post-fix string from left to right.
2. Initialize an empty stack.
3. Repeat the below steps 4 and 5 till all the characters are scanned.
4. If the scanned character is an operand, push it onto the stack.
5. If the scanned character is an operator, and

• If the operator is a unary operator then pop an element from the stack.
• If the operator is binary operator then pop two elements from the stack. AFTER POPPING, APPLY THE OPERATOR TO THOSE POPPED ELEMENTS AND PUSH THE RESULT IN THE STACK.

     6. After all the characters are scanned, we will have only one element in the stack.

     7. This only element is the result of the expression.

Example: Let us see how the above algorithm works with the help of an example. A post-fix expression 1 2 3*+5 –

Initially, our stack is empty. Now the first three characters are scanned 1, 2 and 3 which are operands. They will be pushed into the stack in that order.

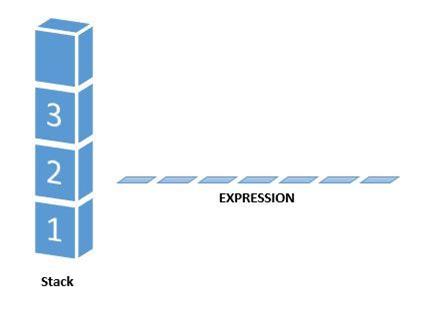
Next character scanned is ” * “, which is an operator. Thus, we pop the top two elements from the stack and perform the * operation with the two operands. The second operand will be the first element that is popped.

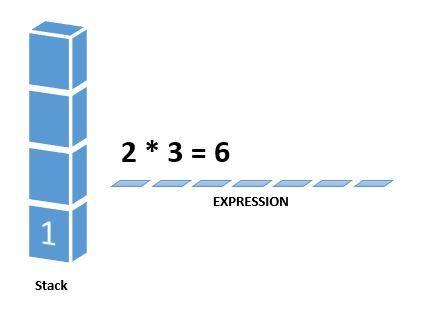
The value of the expression (2 * 3) that has been evaluated (6) is pushed into the stack.

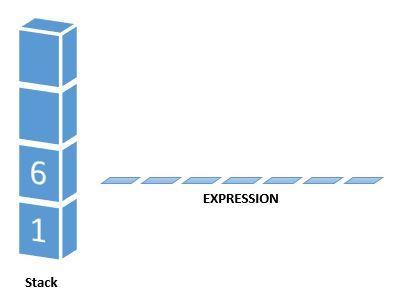
Next character scanned is ” + “ which is an operator. Thus, we pop the two elements from the stack and perform the “+” operation with the two operands. Again remember, the second operand will be the first element that is popped.

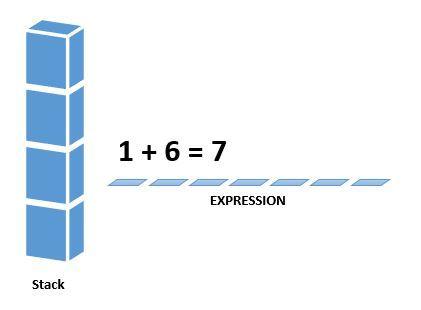
The value of the expression (1 + 6) has been evaluated (7) and has been pushed into the stack.

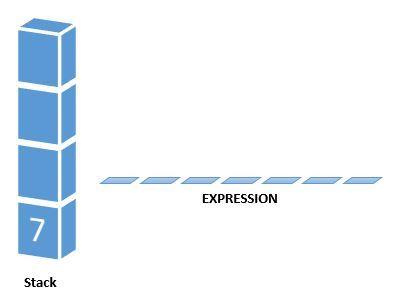
Next character scanned is “5”, which is added to the stack.

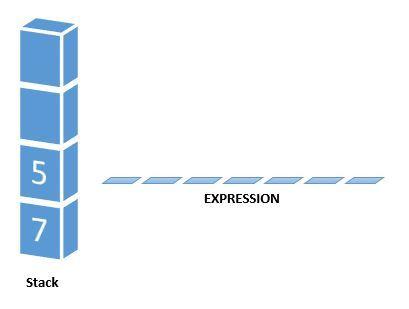
Next character scanned is ” – “, which is an operator. Thus, we pop the top two elements from the stack and perform the “-” operation with the two operands. The second operand will be the first element that is popped.

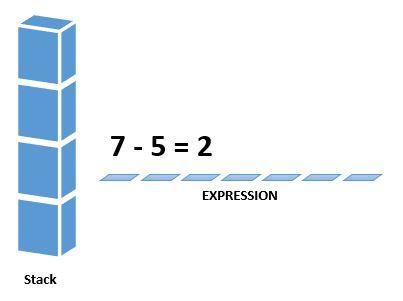
The value of the expression (7 – 5) has been evaluated (2) and is pushed into the stack.

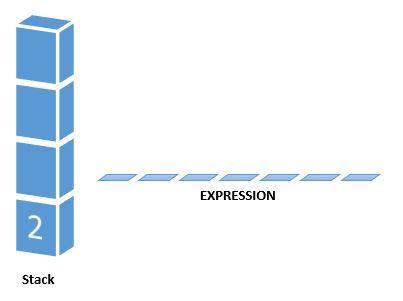
Now since we are out of characters to be scanned, we are left with only one value in the stack. That means that our answer to the post-fix expression is 2.

Listing: Following program is showing infix to postfix conversion using the stack.

#include <string.h>
#include <stdlib.h>

// Stack type
struct Stack
{
int top;
unsigned capacity;
int* array;
};

// Stack Operations
struct Stack* createStack( unsigned capacity )
{
struct Stack* stack = (struct Stack*) malloc(sizeof(struct Stack));

if (!stack) 
return NULL;

stack->top = -1;
stack->capacity = capacity;

stack->array = (int*) malloc(stack->capacity * sizeof(int));

if (!stack->array)
return NULL;
return stack;
}
int isEmpty(struct Stack* stack)
{
return stack->top == -1 ;
}
char peek(struct Stack* stack)
{
return stack->array[stack->top];
}
char pop(struct Stack* stack)
{
if (!isEmpty(stack))
return stack->array[stack->top--] ;
return '$';
}
void push(struct Stack* stack, char op)
{
stack->array[++stack->top] = op;
}

// A utility function to check if the given character is operand
int isOperand(char ch)
{
return (ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z');
}

// A utility function to return precedence of a given operator
// Higher returned value means higher precedence
int Prec(char ch)
{
switch (ch)
{
case '+':
case '-':
return 1;

case '*':
case '/':
return 2;

case '^':
return 3;
}
return -1;
}

// The main function that converts given infix expression
// to postfix expression. 
int infixToPostfix(char* exp)
{
int i, k;

// Create a stack of capacity equal to expression size 
struct Stack* stack = createStack(strlen(exp));
if(!stack) // See if stack was created successfully 
return -1 ;

for (i = 0, k = -1; exp[i]; ++i)
{
// If the scanned character is an operand, add it to output.
if (isOperand(exp[i]))
exp[++k] = exp[i];

// If the scanned character is an ‘(‘, push it to the stack.
else if (exp[i] == '(')
push(stack, exp[i]);

// If the scanned character is an ‘)’, pop and output from the stack 
// until an ‘(‘ is encountered.
else if (exp[i] == ')')
{
while (!isEmpty(stack) && peek(stack) != '(')
exp[++k] = pop(stack);
if (!isEmpty(stack) && peek(stack) != '(')
return -1; // invalid expression 
else
pop(stack);
}
else // an operator is encountered
{
while (!isEmpty(stack) && Prec(exp[i]) <= Prec(peek(stack)))
exp[++k] = pop(stack);
push(stack, exp[i]);
}

}

// pop all the operators from the stack
while (!isEmpty(stack))
exp[++k] = pop(stack );

exp[++k] = '\0';
printf( "%s\n", exp );
}

// program to test above functions
int main()
{
char exp[] = "a+b*(c^d-e)^(f+g*h)-i";
infixToPostfix(exp);
return 0;
}

Output:
abcd^e-fgh*+^*+i-

Listing: C program to evaluate the value of a postfix expression.

// C program to evaluate value of a postfix expression
#include <stdio.h>
#include <string.h>
#include <ctype.h>
#include <stdlib.h>

// The main function that returns value of a given postfix expression
int evaluatePostfix(char* exp)
{
// Create a stack of capacity equal to expression size
struct Stack* stack = createStack(strlen(exp));
int i;

// See if stack was created successfully
if (!stack) return -1;

// Scan all characters one by one
for (i = 0; exp[i]; ++i)
{
// If the scanned character is an operand or number,
// push it to the stack.
if (isdigit(exp[i]))
push(stack, exp[i] - '0');

// If the scanned character is an operator, pop two
// elements from stack apply the operator
else
{
int val1 = pop(stack);
int val2 = pop(stack);
switch (exp[i])
{
case '+': push(stack, val2 + val1); break;
case '-': push(stack, val2 - val1); break;
case '*': push(stack, val2 * val1); break;
case '/': push(stack, val2/val1); break;
}
}
}
return pop(stack);
}

// program to test above functions
int main()
{
char exp[] = "231*+9-";
printf ("Value of %s is %d", exp, evaluatePostfix(exp));
return 0;
}

Output: 
Value of 231*+9- is -4