Breadth First Search

This is a very different approach for traversing the graph nodes. The motive behind the BFS algorithm is to traverse the graph as close as possible to the root node. The queue is used in the implementation of the BFS. Let’s see how BFS traversal works with respect to the following graph:

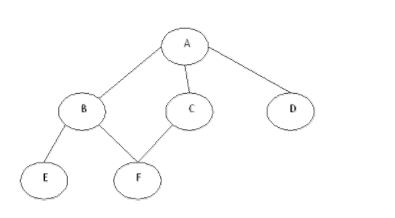
If we do the breadth the traversal of the above graph and print the visited node as the output, it’ll print the following output. “A B C D E F”. The BFS visits the nodes level consecutively, so it will start with level 0 which is the root node, and then it moves to the next levels which are B, C, and D, then the last levels which are E and F.

Algorithm:

1. Push the root node in the Queue.
2. Loop until the queue is empty.
3. Remove the node from the Queue.
4. If the removed node has unvisited child nodes, mark them as visited and insert the unvisited children in the queue.

/*
* C Program to Display the Nodes of a Tree using BFS Traversal 
*                 40
*                 /\
*                20 60
*                /\  \
*              10 30  80
*                      \
*                       90
*/

#include <stdio.h>
#include <stdlib.h>

struct btnode
{ 
    int value; 
    struct btnode *left, *right; 
}; 
typedef struct btnode node;

/* function declarations */
void insert(node *, node *);
void bfs_traverse(node *);

/*global declarations */
node *root = NULL;
int val, front = 0, rear = -1, i;
int queue[20];

void main() 
{ 
    node *new = NULL ; 
    int num = 1; 
    printf("Enter the elements of the tree(enter 0 to exit)\n"); 
    while (1) 
    {     
        scanf("%d",  &num); 
        if (num  ==  0) 
            break; 
        new = malloc(sizeof(node)); 
        new->left = new->right = NULL; 
        new->value = num; 
        if (root == NULL) 
            root = new; 
        else 
        { 
            insert(new, root); 
        } 
    }
    printf("elements in a tree in inorder are\n"); 
    queue[++rear] = root->value;
    bfs_traverse(root);
    for (i = 0;i <= rear;i++)
        printf("%d -> ", queue[i]);
    printf("%d\n", root->right->right->right->value);
}

/* inserting nodes of a tree */
void insert(node * new , node *root) 
{ 
    if (new->value>root->value) 
    {     
        if (root->right == NULL) 
            root->right = new; 
        else 
            insert (new, root->right); 
    } 
    if (new->value < root->value) 
    {     
        if (root->left  ==  NULL) 
            root->left = new; 
        else 
            insert (new, root->left); 
    }     
}

/* displaying elements using BFS traversal */
void bfs_traverse(node *root)
{
    val = root->value;
    if ((front <= rear)&&(root->value == queue[front]))
    {
        if (root->left != NULL)
            queue[++rear] = root->left->value;
        if (root->right != NULL || root->right  ==  NULL)
            queue[++rear] = root->right->value;
        front++;
    }
    if (root->left != NULL)
    {
        bfs_traverse(root->left);
    }
    if (root->right != NULL)
    {
        bfs_traverse(root->right);
    }
}

Output:

Enter the elements of the tree(enter 0 to exit)
40
20
10
30
60
70
80
0
elements in a tree in inorder are
40 -> 20 -> 60 -> 10 -> 30 -> 70 -> 80