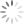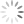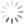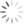B - Tree

In a binary search tree, AVL Tree, Red-Black tree etc., every node can have only one value (key) and a maximum of two children but there is another type of search tree called B-Tree in which a node can store more than one value (key) and it can have more than two children.

To improve the efficiency of operations performed on a tree we need to reduce the height of the tree. Therefore B-Tree is a balanced search tree data structure designed for use with large data sets in secondary storage. B-Tree was developed in the year of 1972 by Bayer and McCreight with the name Height Balanced m-way Search Tree. Later it was named as B-Tree. B-Tree can be defined as follows.

B-Tree is a self-balanced search tree with multiple keys in every node and more than two children for every node.

Here, a number of keys in a node and number of children for a node depends on the order of the B-Tree. Every B-Tree has ordered.

B-Tree of Order m has the following properties.

1 - All the leaf nodes must be at same level.

2 - All nodes except root must have at least [m/2]-1 keys and maximum of m-1 keys.

3 - All nonleaf nodes except root (i.e. all internal nodes) must have at least m/2 children.

4 - If the root node is a nonleaf node, then it must have at least 2 children.

5 - A nonleaf node with n-1 keys must have n number of children.

6 - All the key values within a node must be in Ascending Order.

The following operations are performed on a B-Tree.

• Search

• Insertion

• Deletion

Search Operation in B-Tree

In a B-Tree, the search operation is similar to that of Binary Search Tree. In a Binary search tree, the search process starts from the root node and every time we make a 2-way decision (we go to either left subtree or right subtree). In B-Tree also search process starts from the root node but every time we make an n-way decision where n is the total number of children that node has. In a B-Tree, the search operation is performed with O(log n) time complexity.

The search operation is performed as follows.

• Step 1: Read the search element from the user.

• Step 2: Compare, the search element with the first key value of root node in the tree.

• Step 3: If both are matching, then display "Given node found!!!" and terminate the function.

• Step 4: If both are not matching, then check whether search element is smaller or larger than that key value.

• Step 5: If search element is smaller, then continue the search process in left subtree.

• Step 6: If search element is larger, then compare with next key value in the same node and repeat step 3, 4, 5 and 6 until we found exact match or comparison completed with last key value in a leaf node.

• Step 7: If we completed with last key value in a leaf node, then display "Element is not found" and terminate the function.

Insertion Operation in B-Tree

In a B-Tree, the new element must be added only at a leaf node. That means, always the new key Value is attached to leaf node only.

The insertion operation is performed as follows.

• Step 1: Check whether the tree is Empty.

• Step 2: If the tree is Empty, then create a new node with new key value and insert into the tree as a root node.

• Step 3: If the tree is Not Empty, then find a leaf node to which the new key value can be added using Binary Search Tree logic.

• Step 4: If that leaf node has an empty position, then add the new key value to that leaf node by maintaining the ascending order of key-value within the node.

• Step 5: If that leaf node is already full, then split that leaf node by sending the middle value to its parent node. Repeat the same until sending value is fixed into a node.

• Step 6: If the splitting is occurring to the root node, then the middle value becomes new root node for the tree and the height of the tree is increased by one.

Example: B-Tree of order 4

Each node has four pointers and three keys, and at least two pointers and one key.

• Insert: 5, 3, 21, 9, 1, 13, 2, 7, 10, 12, 4, 8

• Delete: 2, 21, 10, 3, 4

Step 1: Insert 5, 3, 21

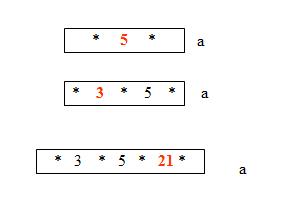
Step 2: Insert 9 (Node splits here and creating two children b and c)

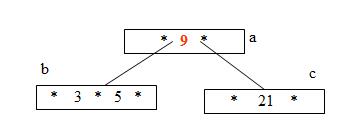
Step 3: Insert 1 and 13 (Nodes b and c have more space to insert more elements)

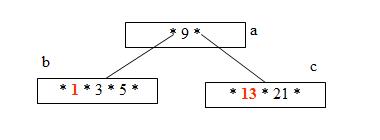
Step 4: Insert 2 (Node b has no more space, so splits creating node d)

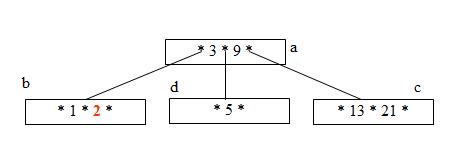
Step 5: Insert 7 and 10 (Nodes d and c have space to add more elements)

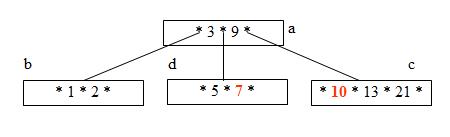
Step 6: Insert 12 (Nodes c must split into nodes c and e)

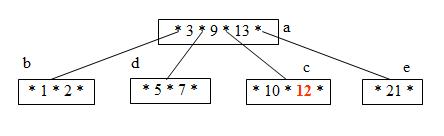
Step 7: Insert 4 (Nodes d has space for another element)

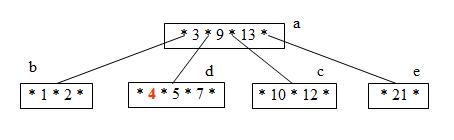
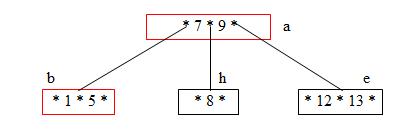
Step 8: Insert 8 (Node d must split into 2 nodes. This causes node a to split into 2 nodes and the tree grows a level. )

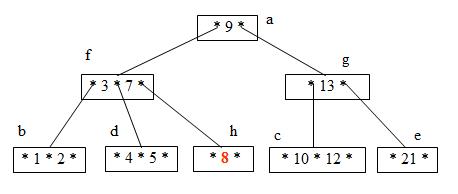
Step 9: Delete 2 (Node b can lose an element without underflow)

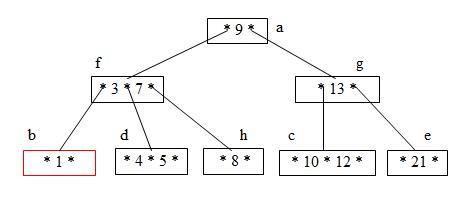
Step 10: Delete 21 (Deleting 21 causes node e to underflow, so elements are redistributed between nodes c, g, and e )

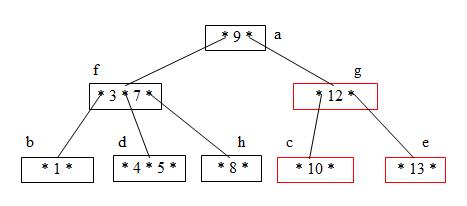
Step 11: Delete 10 (Deleting 10 causes node c to underflow. This causes the parent, node g to recombine with nodes f and a. This causes the tree to shrink one level )

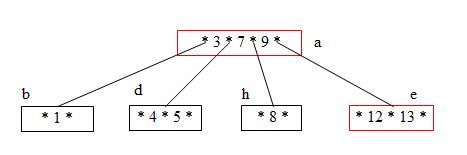
Step 12: Delete 3 (Because 3 is a pointer to nodes below it, deleting 3 requires keys to be redistributed between nodes a and d.)

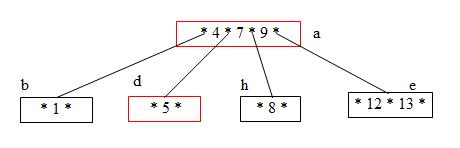
Step 13: Delete 4 (Deleting 4 requires a redistribution of the keys in the subtrees of 4; however, nodes b and d do not have enough keys to redistribute without causing an underflow. Thus, nodes b and d must be combined)